Perpetual Calendars

PERPETUAL CALENDARS................ [Se preferir, veja a página em Português com mais detalhes]

See any year calendar (from 1 AD to infinity). We follow the catholic world rules. Therefore, you'll see in the year 1582, the transition year from Julian to Gregorian Calendar, we didn't have the days 5 to 14 in October month:

Note: If you compare this calendar with the one in Microsoft/Office/Excel, you will find a difference in year 1900. This is a problem in Excel, that incorrectly considers 1900 a leap year. Any attempt to calculate former dates (before 1900 March 1st), starting from Excel calendar, will result 1 day mistake. The bug comes from Lotus 1-2-3 and was purposely implemented in Excel, in order to match both spreadsheets.

You can display 1 to 4713 B.C. calendars, typing 0 for year 1, -1 for year 2, -2 for year 3 a.s.o. until -4712 for year 4713. See details at my page Julian Days. Notice that we're talking about hypothetical calendars, without historical value. Trustworthy historical registers only exist from 4th century A.D.

The world smallest perpetual calendar!

Look at the smallest (and unique) pocket perpetual calendar in the world, from 1 AD to infinity. Print it, cut out and join the three disks with an eyelet or a rivet.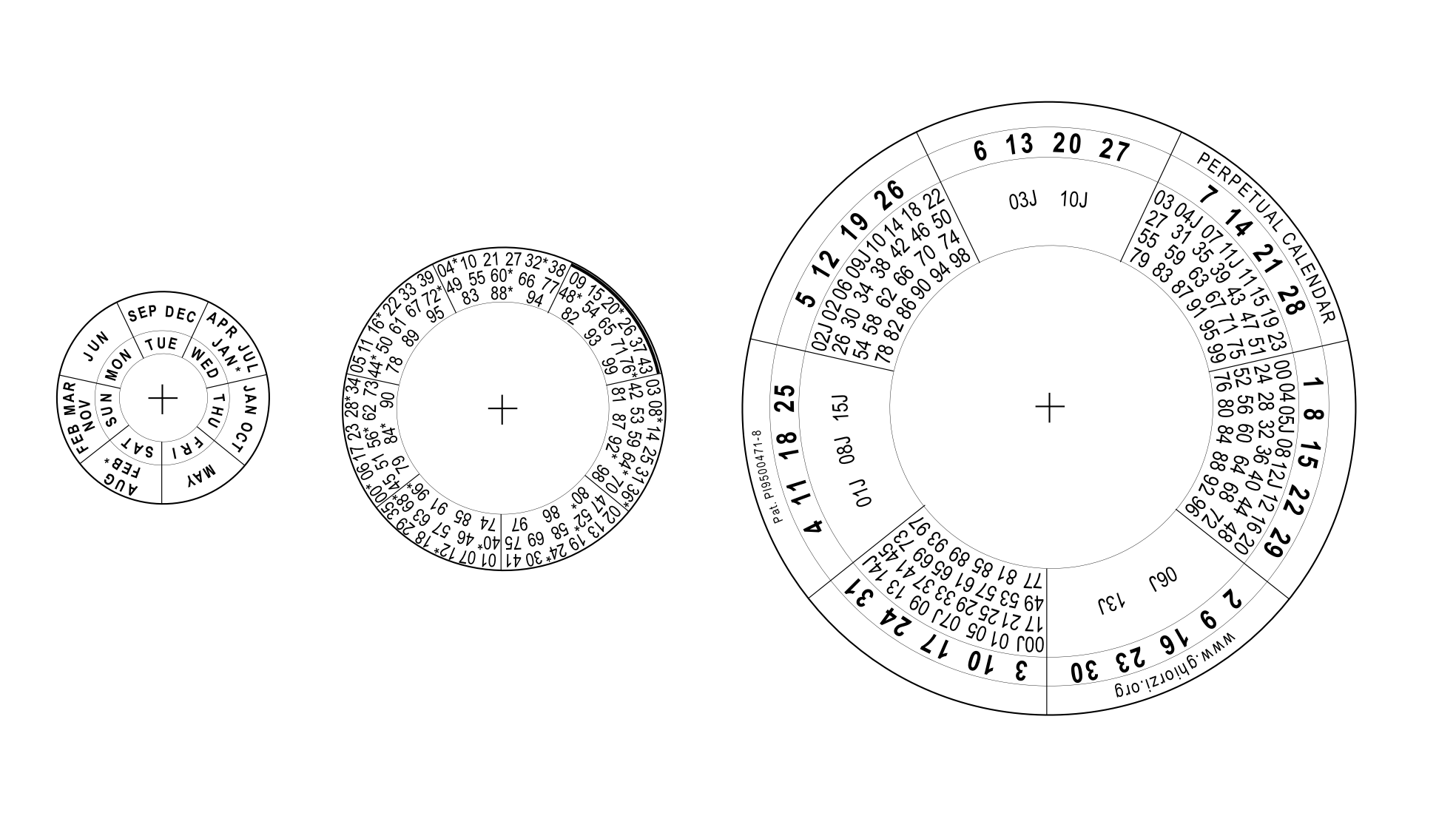

This gadget comprises all thousand/hundred from 00 to 99, allowing, this way, the direct calculation of any past or future date, without any limit. All digits from right to left — from 5th — are indifferent for calculation.

Example: Which day of the week will be August 6, 516763? (516763 - thousand/hundred=67 ten/unit=63). Place arch (A) under thousand/hundred 67 (B). Place AUG (C) under ten/unit 63 (D). You'll see that August 6 (E), 516763 will be Tuesday (F). Note that the outermost and the innermost disks show the whole wished month calendar.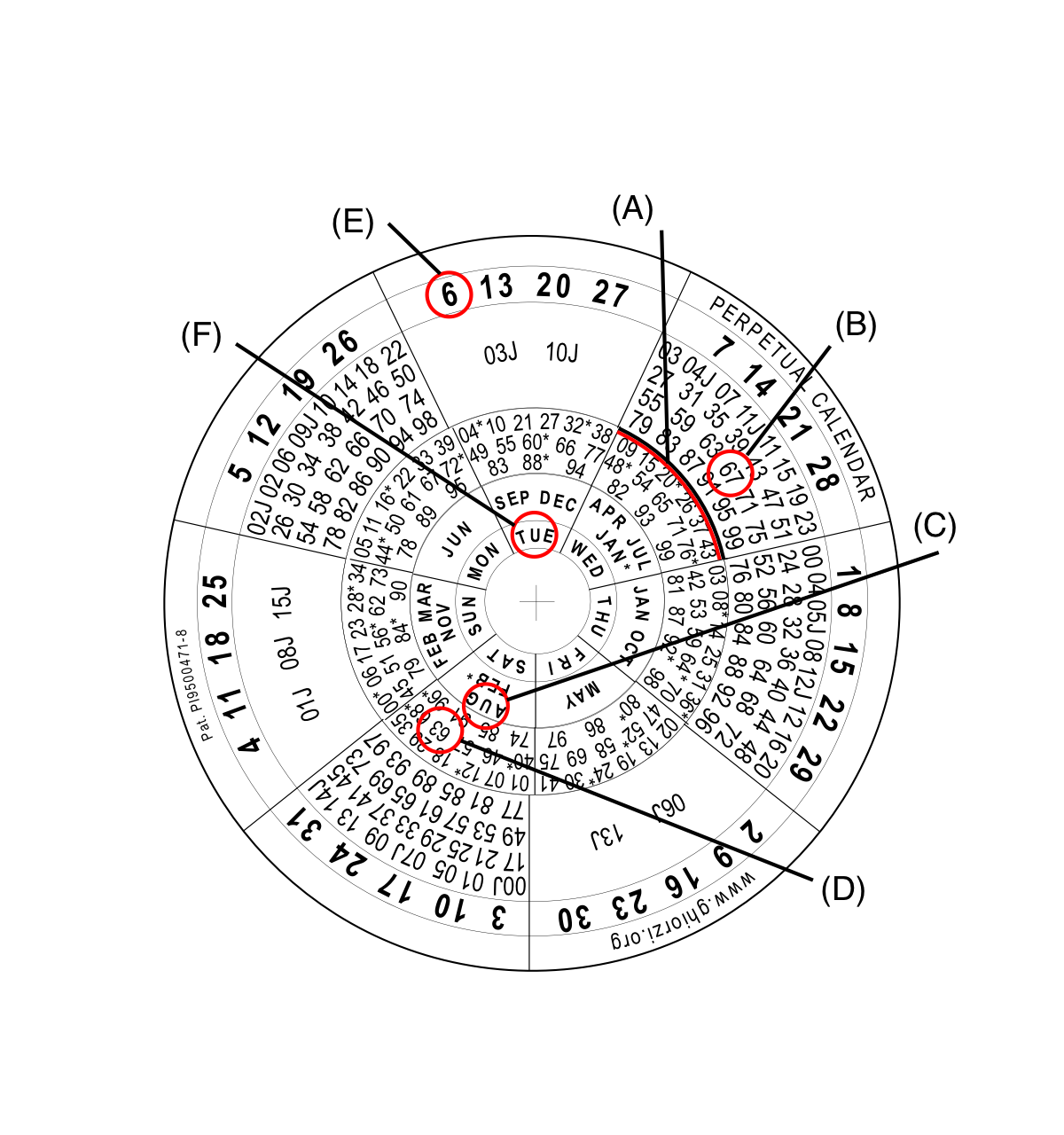

Beware: When you're working with Julian Calendar dates (until October 4, 1582), use exceptionally thousand/hundred numbers followed by the letter "J".
Match leap YEAR and JAN or FEB months marked with an asterisk (*). Note that 1700, 1800, 1900, 2100 and 2200 are not leap years, although divisible by 4.
Note that APR, JUN, SEP and NOV have only 30 days and FEB 28/29 days.
Everything repeats each 4 centuries, on Gregorian Calendar, while repeated each 7 centuries, on Julian Calendar.

In the countries where the Julian Calendar invaded the year 1600, 1700 and so on, it's enough to include 16J in 09J sector, 17J in 10J sector and so on.

Also see other samples of pocket perpetual calendars, if you are an inquisitive person.

A bit of History...
The Julian Calendar began on the 46th year b.C. and ended theoretically on October 4, 1582, a Thursday. And the Gregorian Calendar began on 15 of the same month, a Friday, "erasing" from history the days from October 5 to 14. Portugal and its colonies adopted the Gregorian reform at its beginning, but many nations, including England, did not. Thus, in the English-speaking world, the "missing" days were September 3 to 13, 1752. Around the world we have many exceptions: In Bulgaria, for instance, the "missing" days were April 1 to 13, 1916. Turkey was slower, suppressing the days December 19 to 31, 1926.

Leap years
Although in the Julian Calendar every year that is divisible by 4 is a leap year, the Gregorian Calendar, for greater astronomical precision, provides that years divisible by 4 are leap years, except those ending in "00" and not divisible by 400. That is, the years 1584, 1588... 1600, 2000, 2400 etc. are leap years, but not 1700, 1800, 1900, 2100 etc.. Just because tropic year isn't exactly 365 days and a quarter lasting.

A timely reminder
The 21st century and the 3rd millenium began on January 1, 2001, not 2000.

Mental calculation of the weekday
Surprise your friends, making mental calculation of the weekday for dates from 1901Jan1 to 2099Dec31, using the routine below:

We know that 1901Jan1 was a Tuesday. Let's consider 1=Sun 2=Mon 3=Tue 4=Wed 5=Thu 6=Fri 0=Sat.

a) choose a date from 1901Jan1 to 2099Dec31
b) start from number 3
c) add 1 for each elapsed year (sevens out*)
d) add 1 for each 4 entire elapsed years (sevens out)
e) add the elapsed days of the chosen year (sevens out)
f) the amount (sevens out) will show the weekday

See a practical example:

a) 2013Mar27
b) starting point=3
c) 2013-1901=112 sevens out=0
d) 112÷4=28 sevens out=0
e) 31+28+26=85 sevens out=1
f) 3+0+0+1=4 sevens out=4 (Wednesday)

See another practical example:

a) 1940Apr17
b) starting point=3
c) 1940-1901=39 sevens out=4
d) 39÷4=9,75 and 9 sevens out=2
e) 31+29+31+16=107 sevens out=2
f) 3+4+2+2=11 sevens out=4 (Wednesday)

*sevens out=the remainder of a number divided by seven

The routine above, from 1901 to 2099, is the most searched one. However, you can calculate the weekday from the 1st year of the Christian Era to infinite, if you understand about secular non-leap years (1700, 1800, 1900, 2100, 2200, 2300, 2500 a.s.o.) and about the suppressed 10 days between Julian and Gregorian calendars (1582 October 5 to 14).

We know that 0001Jan1 was, theoretically, a Saturday. Let's consider 1=Sun 2=Mon 3=Tue 4=Wed 5=Thu 6=Fri 0=Sat:

a) choose a date, from 0001Jan1 to infinite
b) get 1 for each elapsed year (sevens out)
c) add 1 for each 4 entire elapsed years (sevens out)
d) add the elapsed days of the chosen year (sevens out)
e) add 6* for each secular non-leap elapsed year (sevens out)
f) add 4** for any date from 1582Nov1 to infinite
g) the amount (sevens out) will show the weekday

*indeed we want to "subtract 1" but it's better to "add 6" (it's the same thing on "sevens out" operations)
**indeed we want to "subtract 10" but it's better to "add 4" (it's the same thing on "sevens out" operations)

See a practical example:
a) 2918Jun3
b) 2918-1=2917 sevens out=5
c) 2917÷4=729,25 and 729 sevens out=1
d) 31+28+31+30+31+2=153 sevens out=6
e) 6x10=60 sevens out=4
f) 4
g) 5+1+6+4+4=20 sevens out=6 (Friday)

See another practical example:
a) 1500Apr21
b) 1500-1=1499 sevens out=1
c) 1499÷4=374,75 e 374 sevens out=3
d) 31+29+31+20=111 sevens out=6
e) 6x0=0
f) 0
g) 1+3+6+0+0=10 sevens out=3 (Tuesday)

See a third practical example, about 21-days-month (1582Oct):
a) 1582Oct22
b) 1582-1=1581 sevens out=6
c) 1581÷4=395,25 e 395 sevens out=3
d) 31+28+31+30+31+30+31+31+30+11=284 sevens out=4
e) 6x0=0
f) 0
g) 6+3+4+0+0=13 sevens out=6 (Friday)